Question

A * X * * Trig Ratios Practice 4 POSSIBL 8 ? 6 In the above triangle, would you use SINE, COSINE, or TANGENT to solve for the missing side (TYPE IN ALL CAPS)? The measure of the missing angle is (ROUND TO THE NEAREST DEGREE). 1 2 3 4 5 6

Answer 1

Right Triangles

The right triangle given in the figure has two given sides of 6 and 8 units respectively.

It's important to identify them as the hypotenuse or one of the legs.

As a rule, the longest side (or the side opposite to the right angle) is the hypotenuse, which measures 8 units.

The other two sides are the legs, one of which measures 6 units.

The required angle (marked as ?) is adjacent to the leg of 6 units.

The only trigonometric ratio that relates the adjacent side of a triangle with the hypotenuse of the triangle is the COSINE.

Now we calculate the measure of the required angle (we'll call it x):

`\cos x=(6)/(8)=0.75`

The angle can be calculated by using the inverse cosine function:

`x=\arccos 0.75`

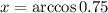
Using a scientific calculator:

x = 41.41°

Rounding to the nearest degree:

x = 41°