Solution
- The function has the following properties:

- The value of "a" is less than 0, therefore, the function has only a maximum value.
- We can find this maximum value by applying the formula given below:

- The Absolute maximum value is 5 and it occurs at x = 0
- Since the function is a quadratic, if it has a maximum value, its minimum value is at negative infinity, while if the function has a minimum value, its maximum value is at positive infinity.
- Thus, we have that:
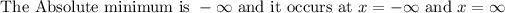
- Strictly speaking, this implies that there is no Absolute minimum since infinity is not on the number line.
- To understand this further, we can plot the graph as follows: