Question

A company manufacturers and sells a electric drills per month. The monthly cost and price-demandequations areC(x) = 57000 + 50x,P = 1900 < 2 < 5000.(A) Find the production level that results in the maximum profit.Production Level = ___(B) Find the price that the company should charge for each drill in order to maximize profit.price = ___

Answer 1

Given the equation:

• C(x) = 57000 + 50x

• p = 190 - x/30

• 0 ≤ x ≤ 5000

Where x is the number is electric drills sold per month.

C(x) is the monthly cost.

Let's solve for the following:

• (A). Find the production level that results in the maximum profit.

To find the production level, we have:

`R(x)=x*P(x)`

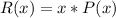
Now, input values into the equation:

`R(x)=x*(190-(x)/(30)_)`

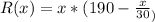
Now, for maximum profit, apply the formula:

`G(x)=R(x)-C(x)`

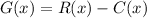
Hence, we have:

`\begin{gathered} G(x)=(x(190-(x)/(30)))-(57000+50x) \\ \\ G(x)=(190x-(x^2)/(30))-(57000+50x) \\ \end{gathered}`

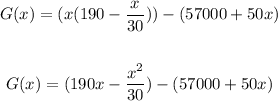
Solving further:

`\begin{gathered} G(x)=190x-(x^2)/(30)-57000-50x \\ \\ G(x)=-(x^2)/(30)+190x-50x-57000 \\ \\ G(x)=-(x^2)/(30)+140x-57000 \\ \\ G(x)=-(x^2)/(30)+140x-57000 \end{gathered}`

Solving further:

Find the derivative

`\begin{gathered} G^(\prime)(x)=-(2x)/(30)+140=0 \\ \\ G^(\prime)(x)=-(2x)/(30)=-140 \\ \\ (x)/(15)=140 \\ \\ x=140*15 \\ \\ x=2100 \end{gathered}`

Therefore, the production that will result in maximum profit is 2100

Production level = 2100

• (,B). Find the price that the company should charge for each drill in order to maximize profit.

We have:

Substitute 2100 for x in p = 190-x/30

`\begin{gathered} p=190-(x)/(30) \\ \\ p=190-(2100)/(30) \\ \\ p=190-70 \\ \\ p=120 \end{gathered}`

Therefore, the price that the company should charge in order to maximize profit is $120 per drill.

ANSWER:

(A). Production level = 2100

(B). Price = $120