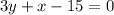Question

Find anequation for the perpendicular bisector of the line segment whose endpoints are(8,9) and (4, -3).

Answer 1

We are given two points that define a line segment: (8,9) and (4,-3)

First, let's find the middle point (or midpoint) between both points

`MP=((8+4)/(2),\frac{9\text{ }-3}{2})=(6,3)`

Since the required equation corresponds to the bisector, it must pass for the point (6,3).

Now we need to find the slope of that line. Since it's perpendicular to the given segment, we can find its slope with the formula

`m^(\prime)=-(1)/(m)`

Where m is the slope of the given line and m' is the slope of its perpendicular line. Let's find m by using the formula:

`m=(y_2-y_1)/(x_2-x_1)=(-3-9)/(4-8)=(-12)/(-4)=3`

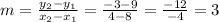
Now find the slope of the perpendicular line

`m^(\prime)=-(1)/(3)`

Now we know one point of the line and its slope, we find the equation with the formula

`y-y_o=m^(\prime)(x-x_0)`

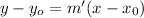
Replacing the values obtained above:

`y-3=-(1)/(3)(x-6)`

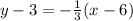
Multiplying by 3

`3(y-3)=-(x-6)=-x+6`

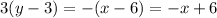
Operating and rearranging

`3y-9=-x+6`
`3y+x-15=0`

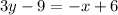
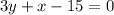
Is the required equation

Solution

`3y+x-15=0`