Given data
*The given true weight is W = 481.0 N
*Difference in weight at the top of the ride is N = 1.50 N
*The angular speed of the Ferris wheel is
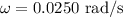
(A)
The apparent weight at the top of the ride is calculated as
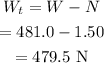
Hence, the apparent weight at the top of the ride is W_t = 479.5 N
(B)
The apparent weight at the bottom of the ride is calculated as
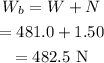
Hence, the apparent weight at the bottom of the ride is W_b = 482.5 N
(C)
The mass of the person is calculated as
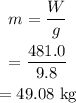
The radius of the Ferris wheel is calculated as
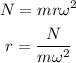
Substitute the known values in the above expression as
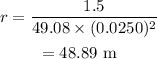
Hence, the radius of the Ferris wheel is r = 48.89 m