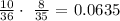To calculate the probability of a specific outcome, we will use the following principle
Probability of a specific outcome = total number of ways in which we get that outcome / total number of possible outcomes.
In this case, we can imagine at first that we are only choosing 1 ball. If we have a total number of balls of n, and we don't care the color of the ball, we could get any of the n balls. So the total number of outcomes for choosing one ball is n. In this case, n is the total number of balls. That is 15 (white) + 8(pink)+3(yellow) + 10(blue) = 36.
Now, note that choosing first 1 blue ball and then 1 pink ball, is the same as considering the case of just choosing 1 ball of a specific color.
For the first case, let us consider the outcome of picking 1 blue ball. At the first draw, we have 36 balls in total and we have 10 blue balls.
So, the probability of choosing 1 blue ball in the first try is 10/36.
Now, assuming we picked one ball that was blue, and we didn't put it back, now we have a total of 35 balls. In this scenario, the probability of picking a pink ball is 8/35 since we have 8 pink balls in a total of 35.
Now, to calculate the probability of having both outcomes is just the multiplication of this two numbers, that is