Given the focus of a parabola as (0,9) and the directrix is y=-9
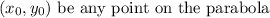
Let us find the distance between
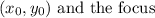
Then we will find the distance between
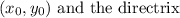
We will then equate these two distance equations and the simplified equation in

is the equation of the parabola
Step 1:
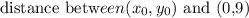
![=\sqrt[]{(x_0}-0)^2+(y_0-9)^2](https://img.qammunity.org/2023/formulas/mathematics/college/ssjs6vilqoy39jv4i96udikwisn1vwsvnd.png)
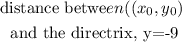
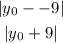
Equating the two distance expressions and square on both sides
![(_{}\sqrt[]{(x_0}-0)^2+(y_0-9)^2)^2=(\lvert y_{0_{}}+9\rvert)^2](https://img.qammunity.org/2023/formulas/mathematics/college/gfevhnssywmhnpvabhrqhpk8rlyhomalh5.png)
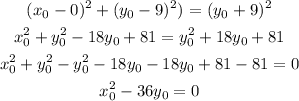
Let us express the equation in terms of
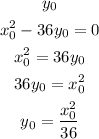
Hence the equation of the parabola is
![undefined]()