To evaluate permutations and combinations, we use the following formulas:
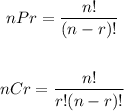
where n is the total number of objects and r is the number of objects selected from the set.
Following the formulas above, we can solve 10C4 and 11P5.
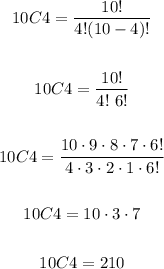
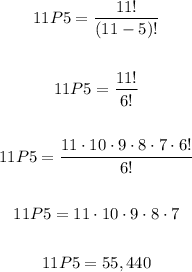
The answers are 210 and 55,440.