Question

A biologist discovered a new species of bacteria. He puts a certain amount of the bacteria into petri dish at t = 0 hours. The amount of bacteria in the petri dish can be modeled by P(t)=165e^0.600t. a) find and interpret P(0)b) according to the model, what will the population of bacteria be after 5 hours and 10 hours?

Answer 1

We are given an equation to model the population of a bacteria after t hours with the following form:

`P(t)=165e^(0.06t)`

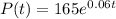
By replacing 0 for t we determine the population of bacteria at the begining of the experiment, then we get:

`\begin{gathered} P(0)=165e^(0.06*0) \\ P(0)=165e^0 \\ P(0)=165*1 \\ P(0)=165 \end{gathered}`

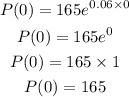
Then P(0) = 165, this means that at the begining of the experiments there were 165 bacterias.

In order to determine the population after 5 hours we just have to replace 5 for t into the model, then we get:

`\begin{gathered} P(5)=165e^(0.06*5) \\ P(5)=165*1.35=222 \end{gathered}`

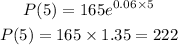
Then, the population of bacteria after 5 hours will be 222. Similarly for 10 hours:

`\begin{gathered} P(10)=165e^(0.06*10) \\ P(10)=300 \end{gathered}`

Then the population of bacteria after 10 hours will be 300