Question

A map shows flagpoles on a coordinate grid. The flagpoles are at (-5, 2), (-5, 6), (-1, 6), and (2, -1). What type of quadrilateral is formed by the flagpoles on the coordinate grid?A. kiteB. rectangleC. rhombusD. squarethank you ! :)

Answer 1

To check what type of quadrilateral we can form with the flagpoles, we can solve and then compare the slopes formed by the sides and the diagonals.

Let's first draw the figure on a Cartesian Plane.

By inspection, the best hypothesis is that the quadrilateral is a kite. So, let's test that first.

We know that the diagonals of a kite are perpendicular so their slopes are negative reciprocals of each other. Let's get the slopes of AC and BD.

`\begin{gathered} m_(AC)=(rise)/(run) \\ \\ m_(AC)=(2-6)/(-5-(-1)) \\ \\ m_(AC)=(-4)/(-4) \\ \\ m_(AC)=1 \end{gathered}`

`\begin{gathered} m_(BD)=(6-(-1))/(-5-2) \\ \\ m_(BD)=(7)/(-7) \\ \\ m_(BD)=-1 \end{gathered}`

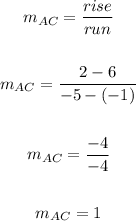
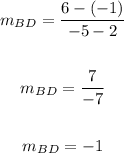
We have now proven that the diagonals are perpendicular. So it's now either a kite or a rhombus.

What distinguishes them is the lengths of their sides. We can use the distance formula to get the lengths of the sides.

`distance=√((x_1-x_2)^2+(y_1-y_2)^2)`
`\begin{gathered} AB=√([-5-(-5)]^2+(2-6)^2) \\ \\ AB=√(0+16) \\ \\ AB=4 \end{gathered}`
`\begin{gathered} BC=√([-5-(-1)]^2+(6-6)^2) \\ \\ BC=√(16+0) \\ \\ BC=4 \end{gathered}`
`\begin{gathered} CD=√((-1-2)^2+[6-(-1)]^2) \\ \\ CD=√(9+49) \\ \\ CD=√(58) \end{gathered}`
`\begin{gathered} AD=√([2-(-5)]^2+(-1-2)^2) \\ \\ AD=√(49+9) \\ \\ AD=√(58) \end{gathered}`

We see here that the consecutive sides (AB and BC, and CD and AD) are congruent, but not all four of them are.

So, the figure is a kite.