Question

. First, calculate the height each can must be, given the radius and volume.

Answer 1

Select the cans with a radius of 2.5 in

Step-by-step explanation:

The volume of a cylinder can be calculated as:

`V=\pi\cdot r^2\cdot h`

Where r is the radius and h is the height of the cans. So, solving for h, we get:

`\begin{gathered} (V)/(\pi\cdot r^2)=(\pi\cdot r^2\cdot h)/(\pi\cdot r^2) \\ (V)/(\pi\cdot r^2)=h \end{gathered}`

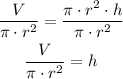
Therefore, the height for each radius is equal to:

`\begin{gathered} h=(90)/(3.14\cdot2^2)=7.16\text{ in} \\ h=\frac{90}{3.14\cdot2.5^2^{}}=4.58\text{ in} \\ h=(90)/(3.14\cdot3^2)=\text{ 3.18 in} \\ h=(90)/(3.14\cdot3.5^2)=\text{ 2.34 in} \end{gathered}`

Then, the lateral surface for each radius can be calculated as:

`A=2\pi rh`

So, the lateral surface for each cylinder is:

`\begin{gathered} A=2(3.14)(2)(7.16)=90in^2 \\ A=2(3.14)(2.5)(4.58)=72in^2 \\ A=2(3.14)(3)(3.18)=60in^2 \\ A=2(3.14)(3.5)(2.34)=51.43in^2 \end{gathered}`

Therefore, the complete table is:

Radius Height Lateral Sur Volume

2 7.16 in 90 in² 90

2.5 4.58 in 72 in² 90

3 3.28 in 60 in² 90

3.5 51.43 in 51.43 in² 90

So, the company should select the can with a radius of 2.5 in because it has a height lower than 5 in and the lateral surface area is the greatest.