Answer:
Select the cans with a radius of 2.5 in
Step-by-step explanation:
The volume of a cylinder can be calculated as:
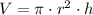
Where r is the radius and h is the height of the cans. So, solving for h, we get:
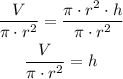
Therefore, the height for each radius is equal to:
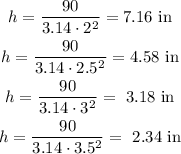
Then, the lateral surface for each radius can be calculated as:
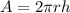
So, the lateral surface for each cylinder is:

Therefore, the complete table is:
Radius Height Lateral Sur Volume
2 7.16 in 90 in² 90
2.5 4.58 in 72 in² 90
3 3.28 in 60 in² 90
3.5 51.43 in 51.43 in² 90
So, the company should select the can with a radius of 2.5 in because it has a height lower than 5 in and the lateral surface area is the greatest.