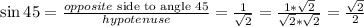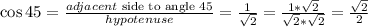Answer:
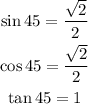
Step-by-step explanation:
Given:
45°-45°-90° triangle.
To find:
The numerical values of the trigonometric ratios.
Let's sketch the given triangle;
Since sides AC and CB are congruent, we can choose the length of their sides to be 1 and go ahead and solve for the length of side AB which is x using the Pythagorean theorem as seen below;
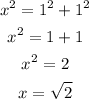
We can now determine the values of each trigonometric ratio as seen below;