Question

30) When a compact disk with a 12.0-cm diameter is rotating at 34.6 rad/s, what are (a) the linear speed and (b) the centripetal acceleration of a point on its outer rim? (c) Consider a point on the CD that is halfway between its center and its outer rim. Without repeating all of the calculations required for parts (a) and (b), determine the linear speed and the centripetal acceleration of this point.

Answer 1

.Given:

The radius of the disk is,

`\begin{gathered} r=(12.0)/(2)\text{ cm} \\ =6.0\text{ cm} \\ =0.06\text{ m} \end{gathered}`

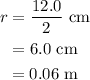
The angular speed is

`\omega=34.6\text{ rad/s}`

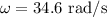
(a)

the linear speed at a point on the outer rim is,

`\begin{gathered} v=\omega r \\ =34.6*0.06 \\ =2.07\text{ m/s} \end{gathered}`

Hence the linear speed is 2.07 m/s.

(b)

The centripetal acceleration is,

`\begin{gathered} a=(v^2)/(r) \\ =(2.07*2.07)/(0.06) \\ =71.4m/s^2 \end{gathered}`

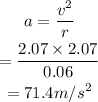
Hence the acceleration is 71.4 m/s^2.

(c)

The linear speed at halfway between the center and the outer rim is

`\begin{gathered} v_1=\omega(r)/(2) \\ =34.6*(0.06)/(2) \\ =1.04\text{ m/s} \end{gathered}`

The centripetal acceleration is,

`\begin{gathered} a_1=\frac{(v_1)^2^{}^{}_{}}{(r)/(2)} \\ =(1.04*1.04)/((0.06)/(2)) \\ =36.0m/s^2 \end{gathered}`

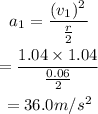
Hence the linear speed is 1.04 m/s, and the centripetal acceleration is 36.0 m/s^2.