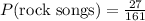Answer
The probability that the first song to play is
SOLUTION
Problem Statement
The question says Neil has 161 songs on a playlist with 18 country, 27 rock, 21 rap, 32 jazz, 8 gospel, 14 latin American, and 41 classical.
We are asked to find the probability that if he puts his playlist on shuffle, that the first song played is a rock song.
Method
To solve the question, we need to know how to find the probability of an event occurring. This is given below:

With this formula, we can easily solve the question.
Implementation
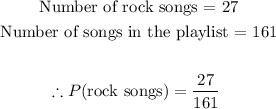
Final Answer
The probability that the first song is a rock song is