Question

The function C(x) = 10x +3,000 represents the cost to produce a number of items. How many items should beproduced so that the average cost is less than $30?Provide your answer

Answer 1

Given:

The cost function is C(x) = 10x + 3000.

Step-by-step explanation:

The equation for the average cost is,

`\begin{gathered} A(x)=(C(x))/(x) \\ =(10x+3000)/(x) \end{gathered}`

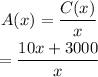
The inequality for x is,

`(10x+3000)/(x)<30`

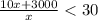
Solve the inequality for x.

[tex]\begin{gathered} \frac{10x+3000}{x}\cdot x<30\cdot x \\ 10x+3000-10x<30x-10 \\ \frac{3000}{20}<\frac{20x}{20} \\ 150So the number of items should be more than 150.