Question

Find the slope of each line and then determine if the lines are parallel perpendicular or neither.If a value is not an integer type it in as a decimal rounded to the nearest hundredth.

Answer 1

ANSWERS

• Slope of line 1: ,8

,

• Slope of line 2: ,-6

,

• The lines are ,neither

Step-by-step explanation

The slope of a line passing through points (x1, y1) and (x2, y2) is,

`m=(y_1-y_2)/(x_1-x_2)`

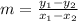
The points given for line 1 are (-8, -55) and (10, 89). The slope of this line is,

`m_1=(-55-89)/(-8-10)=(-144)/(-18)=8`

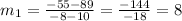
The points given for line 2 are (9, -44) and (4, -14). The slope of this line is,

`m_2=(-44-(-14))/(9-4)=(-44+14)/(5)=(-30)/(5)=-6`

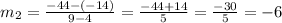
• If two lines are ,parallel, then they have the same slope.

,

• If two lines are ,perpendicular, then their slopes are opposite and reciprocal.

The slopes of these two lines are 8 and -6. These slopes are different and they are neither opposite nor reciprocal. Hence, these lines are neither parallel nor perpendicular.