Question

What transformation takes the graph of f(x)=4x+9 to the graph of g(x)=4x+7 ? translation 2 units righttranslation 2 units lefttranslation 2 units uptranslation 2 units down

Answer 1

1,3,4

Explanation:

keep it easy

Answer 2

If you compare the functions:

`\begin{gathered} f(x)=4x+9 \\ g(x)=4x+7 \end{gathered}`

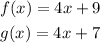
Considering f(x) as the parent function, let's analyze each option:

1) Translation 2 units right.

To translate a function 2 units to the right, you have to subtract 2 to the x-term:

`\begin{gathered} h(x)=f(x-2)=4(x-2)+9 \\ h(x)=4\cdot x-4\cdot2+9 \\ h(x)=4x-8+9 \\ h(x)=4x+1 \end{gathered}`

As you can see the resulting function, h(x), is not equal to g(x), which means that the transformation applied was not a shift 2 units to the right.

2) Translation 2 units to the left

To translate the function two units to the left, you have to add 2 to the x-term:

`\begin{gathered} i(x)=f(x+2)=4(x+2)+9 \\ i(x)=4\cdot x+4\cdot2+9 \\ i(x)=4x+8+9 \\ i(x)=4x+17 \end{gathered}`

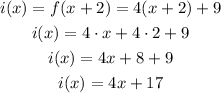
The resulting function, i(x), is not equal to g(x), which means that the transformation applied was not a shift of 2 units to the left.

3) Translation 2 units up

To translate a function 2 units up, you have to add 2 to the function, that is:

`\begin{gathered} j(x)=f(x)+2=(4x+9)+2 \\ j(x)=4x+9+2 \\ j(x)=4x+11 \end{gathered}`

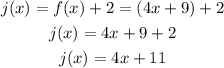
The function j(x) is different from the function g(x), so the transformation applied was not a shift 2 units up.

4) Translation 2 units down

To shift a function two units down, you have to subtract 2 from the function:

`\begin{gathered} k(x)=f(x)-2 \\ k(x)=(4x+9)-2 \\ k(x)=4x+9-2 \\ k(x)=4x+7 \end{gathered}`

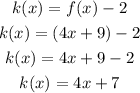
The functions k(x) and g(x) are equal, which means that to determine the function g(x) the function f(x) was translated 2 units down.