Question

Use any convenient method to solve the following system of equations

Answer 1

given the system of equations:

`\begin{gathered} x+4y=9\rightarrow(1) \\ y-2z=-1\rightarrow(2) \\ -4x-7y+6z=-21\rightarrow(3) \end{gathered}`

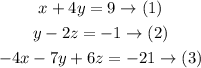
We will solve the system by substitution as follows:

From equation (2)

`y=2z-1\rightarrow(4)`

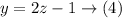
substitute with (y) from equation (4) into equation (1)

`\begin{gathered} x+4(2z-1)=9 \\ x+8z-4=9 \\ x=13-8z\rightarrow(5) \end{gathered}`

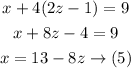
From the equation (4) and (5) substitute with (x) and (y) into equation (3):

`-4(13-8z)-7(2z-1)+6z=-21`

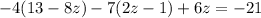
solve the equation to find the value of (z):

`\begin{gathered} -52+32z-14z+7+6z=-21 \\ 24z=-21+52-7 \\ 24z=24 \\ z=(24)/(24)=1 \end{gathered}`

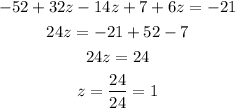
substitute into the equations (4) and (5) to find the values of (x, y)

`\begin{gathered} x=13-8z=13-8\cdot1=5 \\ y=2z-1=2\cdot1-1=1 \end{gathered}`

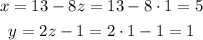
So, the answer will be:

The system has only one solution

x = 5

y = 1

z = 1