Question

Graph the circle x^2+y^2=9

Answer 1

Given:

A circle with the equation:

`x^2+y^2\text{ = 9}`

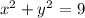
Solution

Recall that the general equation of a circle is of the form:

`(x-a)^2+(y-b)^2=r^2`

Where (a, b) are coordinates of the center and r is the radius of the circle.

Re-writing the given equation using the general form gives us:

`(x-0)^2+(y-0)^2=3^2`

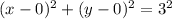
Hence, the center and radius of the circle are (0, 0) and 3 respectively.

The graph of the equation is shown below:

The graph is obtained by first locating the center of the circle (0,0) on the graph. Then, we measure 3 units from the center to construct the required circle.