First, we transform the coordinates of the vertices of P 270° anticlockwise.
The 270° anticlockwise transformation rule, T, is defined as:
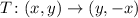
Therefore,
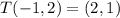
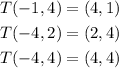
Let the resultant shape be named P'
Hence,
P': (2,1), (4,1) (2,4) (4,4)
Next
We translate the resultant shape downwards by 6 units.
The transformation rule, S, for moving downwards by 6 units is given by:
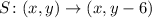
Therefore,
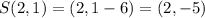
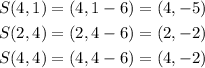
Hence, the image of S on P' is : (2,-2) (2,-5) (4,-2) (4,-5)
This is illustrated by the image below