Question

Jason and Whitney deposit $700.00 into a savings account which earns 11% interest compounded quarterly. They want to use the money in the account to go on a trip in 3 years. How much will they be able to spend?

Answer 1

To solve this problem we need to use the compound interest formula:

`A=P(1+(r)/(n))^(nt)`

Where P is the initial deposit:

`P=700`

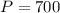
r is the interest rate in decimal form, since the interest rate is 11%, in the decimal form we have:

`r=0.11`

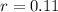
n is the number of times that the interest is compounded in a year, in this case, it is compounded quarterly, and since there are 3 quarters in a year, the interest will be compounded 3 times per year:

`n=3`

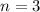
and t is the total time, in this case, 3 years:

`t=3`

Substituting all of these values into the formula to find the Amount "A" they will have after 3 years:

`A=700(1+(0.11)/(3))^(3\cdot3)`

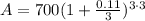
Solving the operations:

`A=700(1+0.03666)^9`
`A=700(1.03666)^9`
`A=700(1.382777)`
`A=967.944`

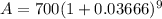
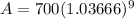
Answer: They will have $967.944 to spend