Question

A test rocket is fired straight up from rest with a net acceleration of 20. 0 m/s2. After 4. 00 seconds the motor turns off, but the rocket continues to coast upward with no appreciable air resistance. What maximum elevation does the rocket reach?.

Answer 1

Approximately
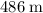`486\; {\rm m}` (assuming that
`g = 9.81\; {\rm m\cdot s^(-2)}`.)

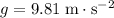Step-by-step explanation:

The rocket started from rest, so the initial velocity would be
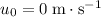`u_(0) = 0\; {\rm m\cdot s^(-1)}`. With an acceleration of
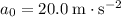`a_(0) = 20.0\; {\rm m\cdot s^(-2)}`, the displacement
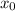`x_(0)` of the rocket at
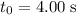`t_(0) = 4.00\; {\rm s}` will be:

`\begin{aligned} x_(0)&= (1)/(2)\, a\, t^(2) \\ &= (1)/(2) * 20.0 * (4.00)^(2) \; {\rm m} \\ &= 160\; {\rm m}\end{aligned}`.

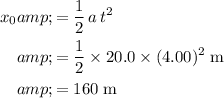In other words, the rocket would have reached a height of
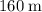`160\; {\rm m}` when the motors turns off.

The velocity of the rocket at that point will be:

`\begin{aligned}v_(0) &= u_(0) + a_(0)\, t_(0) \\ &= 0\; {\rm m\cdot s^(-1)} + (20.0 * 4.00)\; {\rm m\cdot s^(-1) \\ &= 80.0\; {\rm m\cdot s^(-1)}\end{aligned}`.

Since air resistance on the rocket is negligible, the acceleration of the rocket after motor power-off will be
`a_(1) = (-g) = (-9.81)\; {\rm m\cdot s^(-2)` (
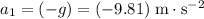`g` is the strength of the gravitational field.)

The rocket started with a velocity of
`{u}_(1) = v_(0) = 80.0\; {\rm m\cdot s^(-1)}` when the motor powers off. When the rocket reaches maximum height, the velocity of the rocket will be
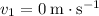`v_(1) = 0\; {\rm m\cdot s^(-1)}`. Apply the SUVAT equation
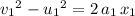`{v_(1)}^(2) - {u_(1)}^(2) = 2\, a_(1)\, x_(1)` to find the additional elevation
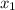`x_(1)` that the rocket will gain after the motor powers off:

`\begin{aligned} x_(1) &= \frac{{v_(1)}^(2) - {u_(1)}^(2)}{2\, a_(1)} \\ &= ((0)^(2) - (80)^(2))/(2 * (-9.81)) \\ &\approx 326\; {\rm m}\end{aligned}`.

Combine
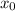`x_(0)` (elevation at motor power-off) and
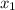`x_(1)` (elevation height gained after motor power-off) to find the overall maximum elevation of the rocket:

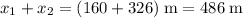`x_(1) + x_(2) = (160 + 326)\; {\rm m} = 486\; {\rm m}`.