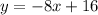Answer: y = –8x + 16
Step-by-step explanation
Given
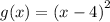
First, we have to know the y-intercept, which is the point where x = 0:
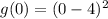

Thus, the y-intercept is (0, 16).
Next, we have to get the derivative of the function, as the tangent line is the derivative:
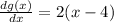
Then, we have to compute the slope:
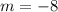
Finally, we find the line in the slope-intercept form (y = mx + b):
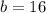
Thus: