Question

You want to be able to withdraw $30,000 from your account each year for 30 years after you retire.You expect to retire in 20 years.If your account earns 6% interest, how much will you need to deposit each year until retirement to achieve your retirementgoals?$Round your answer to the nearest cent.Question Help: Video Post to forum

Answer 1

In this case we are making deposits each year in out account. This will be compounded at a 6% interest.

After 20 years of working and making deposits, the principal accumulated has to be able to give $30,000 per year for 30 years.

We can start with the principal. We assume that during retirement, the account yield 6% interest from the capital still in the account.

Then, we can calculate this principal as the present value of an annuity with payments PMT = $30,000, rate of interest r = 0.06 and n = 30 years.

The calculation is:

`\begin{gathered} PV=PMT\cdot(1-(1+r)^(-n))/(r) \\ PV=30000\cdot(1-(1.06)^(-30))/(0.06) \\ PV\approx30000\cdot(1-0.17411)/(0.06) \\ PV\approx30000\cdot(0.82589)/(0.06) \\ PV\approx30000\cdot13.7648 \\ PV\approx412944.93 \end{gathered}`

Now we know the amount of capital that has to be accumulated with the deposits.

This value is the future value of an annuity of n = 20 years at a rate r = 0.06.

But now, we need to calculate the yearly deposit D.

We can calculate it as:

`\begin{gathered} D=(FV\cdot r)/((1+r)^n-1) \\ D=(412944.93\cdot0.06)/((1.06)^(20)-1) \\ D\approx(24776.70)/(3.207-1) \\ D\approx(24776.70)/(2.207) \\ D\approx11225.73 \end{gathered}`

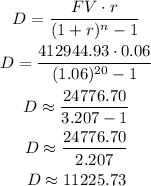
Answer: the yearly deposit has to be $11,225.73.