Question

A new car is purchased for $38, 000 and over time its value depreciates by one hievery 5.5 years. Write a function showing the value of the car after t years, whereannual decay rate can be found from a constant in the function. Round all coefficiin the function to four decimal places. Also, determine the percentage rate of decaper year, to the nearest hundredth of a percent.

Answer 1

`\begin{gathered} P(t)=38,000e^(-0.1260t) \\ rate=11.84\% \end{gathered}`

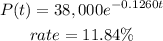
Explanations:

The standard formula for depreciation is expressed as:

`P(t)=P_0(1-r)^t`

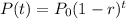
where

• r is the rate

,

• t is the time take

,

• P0 is the original price

If the car depreciates by one half every 5.5years, then P(t) = 19000

Given

Po = $38000

t = 5.5 years

P(t) = 38000/2 = $19000

Substitute

`\begin{gathered} 19000=38000(1-r)^(5.5) \\ (1)/(2)=(1-r)^(5.5) \end{gathered}`

Determine the percentage rate "r"

`\begin{gathered} ln(0.5)=5.5ln(1-r) \\ ln(1-r)=(ln(0.5))/(5.5) \\ ln(1-r)=-(0.6931)/(5.5) \\ ln(1-r)=-0.1260 \\ 1-r=e^(-0.1260) \\ 1-r=0.8816 \\ r=1-0.8816 \\ r=0.1184 \\ r=11.84\% \end{gathered}`

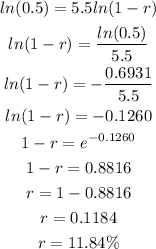
Hence the percentage rate of decay per year is 11.84%

Determine the function showing the value of the car after t years

`\begin{gathered} P(t)=P_o(1-r)^t \\ P(t)=38000(1-0.1184)^t \\ P(t)=38000e^(-0.1260t) \end{gathered}`