Question

What are the first three terms of the Gp of which the common ratio is -⅔ and S6 is 133

Answer 1

Given that S6 is 133 and the common ratio (r) is -2/3.

We know that the sum of n terms of a gp whose common ratio is less than 1 is

`S_n=(a(1-r^n))/((1-r))`

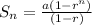
So,

`\begin{gathered} 133=(a(1-(-(2)/(3))^6))/(1-(-(2)/(3))) \\ 133=(a(1-(64)/(729)))/(1+(2)/(3)) \\ 133=(a((665)/(729)))/((5)/(3)) \\ 133=(a(133))/(243) \\ a=243 \end{gathered}`

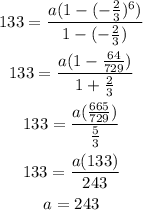
Now, we have known that the first term of the gp is 243.

So, the second term is:

`ar=243*(-(2)/(3))=-162`

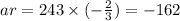
The third term is:

`ar^2=243*(-(2)/(3))^2=108`

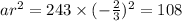
Thus, the first three terms are 243, -162, 108.