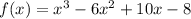Since f(x) is a polynomial with 3rd degree, then it will have 3 roots (zeroes)
One of them is real and the other two are complex conjugate roots
Since the real root is 4, then
x = 4
Since the complex root is (1 - i), then
The other root will be the conjugate of it (1 + i)
x = (1 - i)
x = (1 + i)
To find f(x) we will multiply the three factors of it
We can get the factors from the zeroes

Subtract 4 from both sides
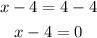
The first factor is (x - 4)
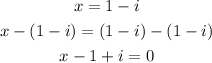
The second factor is (x - 1 + i)
The third factor is (x - 1 - i)
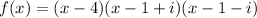
We will multiply them to find f(x)
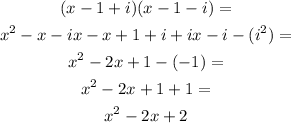
Multiply it by (x - 4)
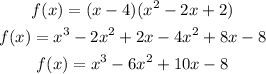
The answer is