Answer:
a) 0.47 s
b) 1.1 m
c) 7.2 m
d) 15.9 m/s
Step-by-step explanation:
Part a)
To find the total air time, we will use the equation for the vertical movement of the stone, so
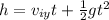
Where h is the height, viy is the initial vertical velocity and it is 0 m/s, g is the gravity and t is the time.
Replacing h = 1.1 m, viy = 0 m/s and g = 9.8 m/s² and solving for t, we get
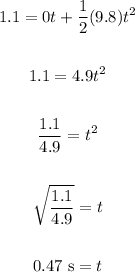
Therefore, the total air time was 0.47 s
Part b)
The stone leaves horizontally, so the maximum height is the initial height of 1.1 m
Part c)
The range can be calculated using the following equation
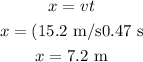
Therefore, the horizontal distance traveled was 7.2 m
Part d)
First, we will calculate the final vertical velocity as
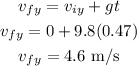
Then, the final vertical velocity was 4.6 m/s and the horizontal velocity was 15.2 m/s, so the final velocity was
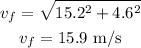
Therefore, the answers are
a) 0.47 s
b) 1.1 m
c) 7.2 m
d) 15.9 m/s