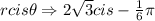Step-by-step explanation:
The polar form of a complex number z = x + iy is calculated using the formula below:
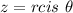
where:
r = sqrt root of (x² + y²) and is also considered as the modulus of the complex number
θ = tan^-1 (y/x) is the argument of the complex number.
So, for the first complex number 3 - √3i, let's convert this to polar form in which x = 3 and y = - √3.
To convert, let's solve for the "r" or the modulus first.
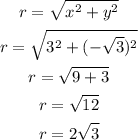
The modulus is 2√3.
Let's solve for the θ or the argument.
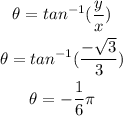
The argument is -1/6π.
Plugging in the modulus and argument to the abbreviated polar form of a complex number, the result is: