Question

What is the retraction force (in lbf) of an 8 inch diameter cylinder with a 6 inch rod and pressure of 600psi?

Answer 1

We are asked to determine the retraction force on a cylinder. A diagram of the problem is the following:

To determine the retraction force we will use the fact that the pressure is defined as:

`P=(F)/(A)`

Where:

`\begin{gathered} P=\text{ pressure} \\ F=\text{ Force} \\ A=\text{ }Area \end{gathered}`

To solve for the force we will multiply both sides by "A":

`PA=F`

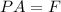
The area is given by the following:

We have the circle of the cylinder and the circle formed by the rod. Therefore, the area in contact with the pressure is equivalent to subtracting the area of the 6 inches circle from the area of the 8 inches circle like this:

`A=A_8-A_6`

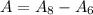
The area of a circle is given by:

`A=\pi(D^2)/(4)`

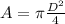
Where "D" is the diameter. Replacing in the formula for the area;

`A=(\pi D^2_8)/(4)-(\pi D^2_6)/(4)`

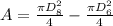
Replacing the diameters:

`A=(\pi(8in)^2)/(4)-\frac{\pi(6in)^2^{}_{}}{4}`

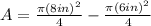
Solving the operations:

`A=22in^2`

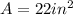
Replacing in the formula for the force we get:

`(300(lb_f)/(in^2))(22in^2)=F`

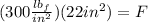
Solving the operations:

`6600lb_f=F`

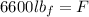
Therefore, the retraction force is 6600 lbf.