Question

The coordinates of the vertices of the preimage of a parallelogram are (1,5), (3, 3), (3, 7), and (5,5). The coordinates of the vertices of the image are (-5,3), (-3,1),(-3,5), and (-1,3). How far and in what direction was the parallelogram translated?

Answer 1

The parallelogram is translated about 6.33 units far, 2 units left and 4 units downwards

Step-by-step explanation:

Given:

The coordinates of the vertices of the preimage of the parallelogram are:

(1,5), (3,3), (3,7), and (5,5)

The coordinates of the vertices of the image are:

(-5,3), (-3,1), (-3,5), and (-1,3).

We want to know how far and in what direction the parallelogram was translated.

Looking at the given coordinates, we see that there is an equal distance between a coordinate in the image with the corresponding image.

(1,5) and (-5,3)

(3,3) and (-3,1)

(3,7) and (-3,5)

(5,5) and (-1,3)

all have equal distances between them.

So, knowing the distance of one suffices for all.

The distance between two points is given by the formula:

`D=\sqrt[]{(y_2-y_(1)^2)+(x_2-x_1)^2}`

Using the coordinates (1,5) and (-5,3)

`\begin{gathered} x_1=1 \\ y_1=5 \\ x_2=-5 \\ y_2=3 \end{gathered}`

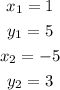
So

`\begin{gathered} D=\sqrt[]{(3-5)^2+(-5-1)^2} \\ \\ =\sqrt[]{(-2)^2+(-6)^2} \\ \\ =\sqrt[]{4+36} \\ \\ =\sqrt[]{40} \\ \\ =6.33\text{ units} \end{gathered}`

The Direction:

The translation is 2 units left, and 4 units downward