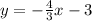Question

Write the equation in slope-intercept form and then graph the equation that passes through (−3, 1) and is parallel to y = − 4/3 x − 1

Answer 1

The equation in slope-intercept form is

`\begin{gathered} y=mx+b \\ \text{Where} \\ m\colon\text{ slope of the line} \\ b\colon\text{ }y\text{-intercept} \end{gathered}`

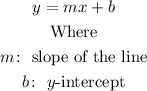
On the other hand, two lines are parallel if they have the same slope, so the new line will also have slope m=-4/3. Then, using the equation point slope you have

`\begin{gathered} y-y_1=m(x-x_1) \\ \text{Where} \\ (x_1,y_1)\text{ }\colon\text{ }A\text{ point through which the line passes} \\ \text{ So,} \\ y-y_1=m(x-x_1) \\ y-1=-(4)/(3)(x-(-3)) \\ y-1=-(4)/(3)(x+3) \\ y-1=-(4)/(3)x-(4)/(3)\cdot3 \\ y-1=-(4)/(3)x-4 \\ \text{ Add 1 to both sides of the equation} \\ y-1+1=-(4)/(3)x-4+1 \\ y=-(4)/(3)x-3 \end{gathered}`

Therefore, the equation in slope-intercept form that passes through (−3, 1) and is parallel to y = − 4/3 x − 1​ is

`y=-(4)/(3)x-3`