Let the width of the rectangular field = x meters
Since the field is 40 m longer than it is wide,
• Length of the rectangular field = x+40 meters
Given, the perimeter of the field = 580 m
Perimeter of a rectangle = 2(Length + Width)
Substitution of the given values gives:
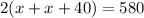
Next, we solve for x

Therefore, the dimensions of the field are:
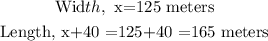
The rectangular field is 125 meters wide and 165 meters long.