Question

Determine whether the equation defines Y is a function of XPlease explain

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given equation

`x^4+y^7=6`

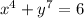
STEP 2: Express y as the subject of the equation

`\begin{gathered} x^4+y^7=6 \\ \text{Subtract }x^4\text{ from both sides} \\ x^4+y^7-x^4=6-x^4 \\ y^7=6-x^4 \\ \text{ Find the 7th root of both sides} \\ y^{}=\sqrt[7]{6-x^4} \end{gathered}`

STEP 3: Define when y is a function of x

y is a function of x if for every value of x in the domain of definition, where x takes its values, there corresponds only one value of y. Not every set of ordered pairs defines a function. Not all equations with the variables x and y define a function. If an equation is solved for y and more than one value of y can be obtained for a given x, then the equation does not define y as a function of x. So the equation is not a function.

`\begin{gathered} y^{}=\sqrt[7]{6-x^4} \\ \text{when x=1} \\ y^{}=\sqrt[7]{6-1^4} \\ y=\sqrt[7]{6-1^{}}=\sqrt[7]{5^{}}=1.2585 \\ \text{when x=2} \\ y^{}=\sqrt[7]{6-2^4}=\sqrt[7]{6-16}=\sqrt[7]{-10}=-1.3895 \end{gathered}`

Since it can be seen that for every value of x, there is a single value for y, hence it can be concluded that "The equation defines y as a function of x.