A standard deck contains 52 cards; without all the aces and twos, it would have 52-8=44 cards in total.
a) There are 13 heart cards in a normal deck; in this one, there are 13-2=11 heart cards; therefore,
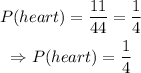
The answer to part a) is P(heart)=1/4.
b) Half of the cards in a standard deck are black; since we removed 4 red cards and 4 black cards,
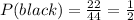
P(black)=1/2
c) There are 12 face cards in a normal deck and none of them was removed; thus,
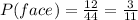
P(face card)=3/11
d) In general, if A is an event,
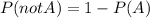
Therefore, in our case,
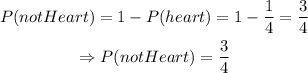
P(not heart)=3/4