Question

Use the given partition and sample points to approximate the definite integral off(x) = x2 + 4x + 6 on the indicated interval.

Answer 1

Given:

`f(x)=x^2+4x+6`

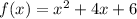
To approximate the definite integral using given partition and sample points, we use the formula

`\Sigma f(x_i)\Delta x_i`

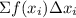
From the interval given,

`\begin{gathered} -3<-2<-1<0<1,\text{ then } \\ \Delta x_i=1 \\ at\text{ every partition} \end{gathered}`
`\begin{gathered} \Sigma f(x_i)\Delta x_i=f(1)\Delta x_1+f(0)\Delta x_2+f(-1)\Delta x_3+f(-2)\Delta x_4 \\ \\ \sin ce\text{ }\Delta x_i=1,\text{ then} \\ \Sigma f(x_i)\Delta x_i=f(1)+f(0)+f(-1)+f(-2) \end{gathered}`
`\begin{gathered} f(x)=x^2+4x+6 \\ f(1)=1^2+4(1)+6=1+4+6=11 \\ f(0)=0^2+4(0)+6=0+0+6=6 \\ f(-1)=(-1)^2+4(-1)+6=1-4+6=3_{} \\ f(-2)=(-2)^2+4(-2)+6=4-8+6=2 \end{gathered}`

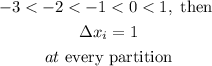
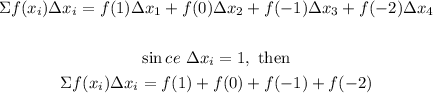
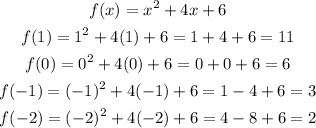
Hence, the approximate value of the definite integral is;

`\begin{gathered} \Sigma f(x_i)\Delta x_i=f(1)+f(0)+f(-1)+f(-2) \\ \Sigma f(x_i)\Delta x_i=11+6+3+2 \\ \Sigma f(x_i)\Delta x_i=22 \end{gathered}`

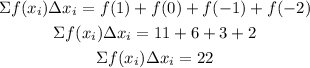
Therefore, the approximate value of the definite integral is 22.