Let x be the random variable representing the weight of the peaches produced by the company. Since they are normally distributed and the population mean and standard deviation are known, we would apply the formula for normal distribution which is expressed as
z = (x - mean)/standard deviation
z represents the z score
From the informtion given,
mean = 12
standard deviation = 0.6
The probability that the weight of a selected peach is more than 12 ounce is expressed as
P(x > 12)
This is also expressed as
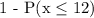
For x = 12,
z = (12 - 12)/0.6 = 0
Looking at the normal distribution table, the probability corresponding to the z score of 0 is 0.5
P(x > 12) = 0.5
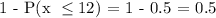
Since the number of samples is 1000, then the number of peaches expected to have any weights of more than 12 ounces is
0.5 * 1000 = 500
500 peaches are expected to have any weights of more than 12 ounces