Question

Solving Right triangles where the two legs are given.Equation no. 1: Triangle ABC is right angled at C. if a = 18.5 and b = 14.2. Find ∠A, ∠B and c.Provide your summary.

Answer 1

• m∠A=52.5°

,

• m∠B=37.5°

,

• c=23.3

Explanation:

Given the right triangle below:

(a)∠A

• The side length ,opposite angle A ,=18.5

,

• The side length ,adjacent to angle A ,=14.2

From trigonometrical ratios:

`\begin{gathered} \tan A=(BC)/(AC) \\ \implies\tan A=(18.5)/(14.2) \\ A=arctan((18.5)/(14.2)) \\ m\angle A=52.5\degree \end{gathered}`

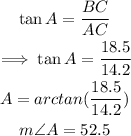
The measure of angle A is 52.5°.

(b)∠B

• The side length ,opposite angle A ,=14.2

,

• The side length ,adjacent to angle A ,=18.5

From trigonometrical ratios:

`\begin{gathered} \tan B=(AC)/(BC) \\ \implies\tan B=(14.2)/(18.5) \\ B=arctan((14.2)/(18.5)) \\ m\angle B=37.5\degree \end{gathered}`

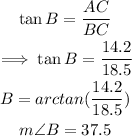
The measure of angle B is 37.5°.

(c)To find the length of c, apply the Pythagorean theorem.

`\begin{gathered} c=√(a^2+b^2) \\ c=√(18.5^2+14.2^2)=√(543.89) \\ c\approx23.3 \end{gathered}`

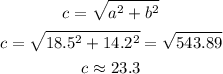
Thus:

• m∠A=52.5°

,

• m∠B=37.5°

,

• c=23.3