1 Answer

Ask a Question

Bill Mei · Answer 1 · 2023-11-17T16:42:38+0000

Solution

The population standard deviation is given as

$\sigma=\sqrt[]{(\sum ^N_(i\mathop=1)(x_i-\mu)^2)/(N-1)}$

First, we calculate the mean;

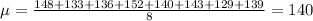
$\mu=(148+133+136+152+140+143+129+139)/(8)=140$

Thus, the standard deviation is;

$\begin{gathered} \sigma^2==((148-140)^2+(133-140)^2+(136-140)^2+(152-140)^2+(140-140)^2+(143-140)^2+(129-140)^2+(139-140)^2)/(7) \\ \sigma^2=57.7 \\ \sigma=\sqrt[]{57.7} \\ \sigma=7.6 \end{gathered}$

The confidence interval for standard deviation is given by;

[tex]s\sqrt[]{\frac{n-1}{\chi^2_{n-1,\frac{\alpha}{2}}}_{}}<\sigmaOption A is the correct option.

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions