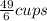Given that:
- The recipe calls for this amount of flour for 3 dozen cookies:
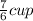
- Cassandra plans to make 21 dozen cookies.
Let be "x" the number of cups of flour she needs to make 21 dozen cookies.
Using the data given in the exercise, you can set up the following proportion:
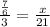
Now you have to solve for "x":
1. You can rewrite the expression on the left side as follows:

2. Simplify by multiplying the fractions on the left side:
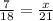
3. Multiply both sides of the equation by 21:
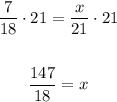
4. You can reduce the fraction by dividing the numerator and the denominator by 3:
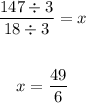
Hence, the answer is: