Question

Pls answer the b. What is the three various values of a and b

Answer 1

Given:

The right triangle is,

We know that, the sum of angles of triangle is 180 degree.

As it is right triangle the measure of one angle is 90 degree.

`\begin{gathered} \angle a+\angle b+90^(\circ)=180^(\circ) \\ \angle a+\angle b=180^(\circ)-90^(\circ) \\ \angle a+\angle b=90^(\circ) \end{gathered}`

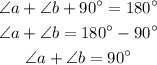
All that values which satisfy the above equation will be the possible values of a and b.

The three possible values of a and b will be,

`\begin{gathered} \angle a=50^(\circ),\angle b=40^(\circ) \\ \angle a=30^(\circ),\angle b=60^(\circ) \\ \angle a=60^(\circ),\angle b=30^(\circ) \end{gathered}`

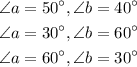
Using these three values complete the chart,

1)

`\begin{gathered} \angle a=50^(\circ),\angle b=40^(\circ) \\ \angle a+\angle b=90^(\circ) \\ \sin (a+b)=\sin (90^{\circ^{}})=1 \\ \sin (a)=\sin (50^(\circ))=0.766\text{ }.\ldots\text{(up to 3 decimal place)} \\ \sin (b)=\sin (40^(\circ))=0.643\ldots\text{.(up to 3 decimal places)} \\ \sin (a)+\sin (b)=0.776+0.643=1.419 \end{gathered}`

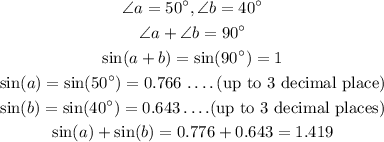
2)

`\begin{gathered} \angle a=30^(\circ),\angle b=60^(\circ) \\ \angle a+\angle b=90^(\circ) \\ \sin (a+b)=\sin (90^{\circ^{}})=1 \\ \sin (a)=\sin (30^(\circ))=(1)/(2) \\ \sin (b)=\sin (60^(\circ))=\frac{\sqrt[]{3}}{2} \\ \sin (a)+\sin (b)=(1)/(2)+\frac{\sqrt[]{3}}{2}=\frac{1+\sqrt[]{3}}{2} \end{gathered}`

3)

`\begin{gathered} \angle a=60^(\circ),\angle b=30^(\circ) \\ \angle a+\angle b=90^(\circ) \\ \sin (a+b)=\sin (90^{\circ^{}})=1 \\ \sin (a)=\sin (60^(\circ))=\frac{\sqrt[]{3}}{2} \\ \sin (b)=\sin (30^(\circ))=(1)/(2) \\ \sin (a)+\sin (b)=\frac{\sqrt[]{3}}{2}+(1)/(2)=\frac{\sqrt[]{3}+1}{2} \end{gathered}`