We can use a linear equation to represent this situation.
In this case the linear equation y= mx + b can be expressed as C(t) = mt + b ( m: slope of the line or the charge for each minute and b is the y-intercept or the monthly fee)
We have to find the slope of the line with the points (400, 147) and (860, 285)
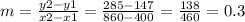
Then, we can find the monthly fee replacing the slope and one of the points in the linear equation. Let us use the point (400,147).
147 = 0.3(400) + b
147 = 120 + b (Multiplying)
27 = b (Subtracting 120 from both sides of the equation)
The answer is C(t)= 0.3t + 27 (t in minutes)