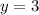Question

Find all horizontal and vertical asymptotes (if any). (If an answer does not exist, enter DNE.)s(x) = 6x2 + 12x2 + 3x − 2vertical asymptote x= (smaller value)vertical asymptote x= (larger value)horizontal asymptote y=

Answer 1

The equations of the vertical asymptotes are the values of the zeroes of the denominator

The given algebraic rational function is

`s(x)=(6x^2+1)/(2x^2+3x-2)`

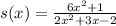
Equate the denominator by 0 to find its roots

`2x^2+3x-2=0`

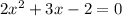
Factor the left side

`\begin{gathered} 2x^2=(2x)(x) \\ -2=(-1)(2) \\ (2x)(2)+(x)(-1)=4x-x=3x \\ 2x^2+3x-2=(2x-1)(x+2) \\ (2x-1)(x+2)=0 \end{gathered}`

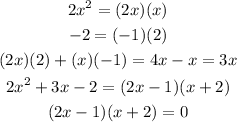
Equate each factor by 0

`\begin{gathered} 2x-1=0 \\ 2x-1+1=0+1 \\ 2x=1 \\ (2x)/(2)=(1)/(2) \\ x=(1)/(2) \end{gathered}`
`\begin{gathered} x+2=0 \\ x+2-2=0-2 \\ x=-2 \end{gathered}`

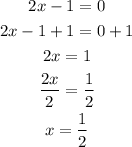
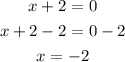
Then the equations of the vertical asymptotes are

`\begin{gathered} x=-2\rightarrow smaller \\ \\ x=(1)/(2)\rightarrow larger \end{gathered}`

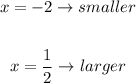
To find the horizontal asymptote

Since the greatest power of up and down is 2

Then divide the coefficients of x^2 up by down

Since the coefficient of x^2 up is 6

Since the coefficient of x^2 down is 2

Since 6/2 = 3

Then the equation of the horizontal asymptote is

`y=3`