Question

Standard from equations

Answer 1

We want to know which of the following statements is/are true about the equation of the parabola

I. In standard form

`y=ax^2+bx+c,a<0\text{ and c }>0`

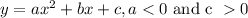
Now, the equation above is truely the equation of a parabola in standard form.

a is less than zero, this means a is negative, this is true, that is why the curve is "n" shaped. If a was positive, the curve would be a "u" shape.

c is greater than 0, now, c is the incerpt on the y-axis, that is where the curve cuts the y-axis. You can see from the graph that, that part is greater than zero,

Hence statement I is true

II. In vertex form

`y=a(x-h)^2+k,h>0\text{ and k }>0`

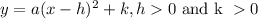
The equation above is true for equation of a parabola in vertex form.

h and k are the coordinates of the vertex. The vertex is the curved part of the graph at the top, the coordinates here are greater than zero for both the x and the y values. Making both h and k greater than zero.

Hence statement II is true

III. In factored form

`y=a(x-p)(x-q)`

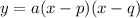
The factored form looks that way, p and q represents the roots of the equation, where the graph cuts the x-axis.

If you look well, you will see that the curve cuts the x-axis at a part which is negative (less than zero) and a part which is positive (greater than zero).

So p and q will not have the same sign. One will be positive and the other will be negative.

Hence statement III is false.

So the answer is I and II only option D