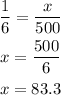Question

Victoria spends 30 spinner song 500 times. Solve a proportion to predict the number of times the sum is 4, 5, or 6.enter the correct answers in the boxes

Answer 1

In this probelm to get a sum that is equal to 6 we have to spin and have 3 in bout spiners so: the probability to have 3 in the first one is:

1/6

and in the secon one is:

1/3

So in total there is a probability of:

`(1)/(3)\cdot(1)/(6)=(1)/(18)`

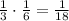
This means that each 18 time he spin the spiners one will be equal to 6 so:

However another option to get 6 is that in the first spiner you have 5 and in the second one you have 1 and the probabilities will be the same so:

`(1)/(3)\cdot(1)/(6)=(1)/(18)`

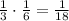
and the last chance to have 6 is if in the first spiner we get 4 and in the secon one we get 2 and the probability will be the same so:

`(1)/(3)\cdot(1)/(6)=(1)/(18)`

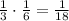
So the probabilitie to have 6 in the sum will be the addition of the probabilites so:

`(1)/(18)+(1)/(18)+(1)/(18)=(3)/(18)=(1)/(6)`

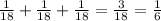
So the proportion will be:

`\begin{gathered} (1)/(6)=(x)/(500) \\ x=(500)/(6) \\ x=83.3 \end{gathered}`