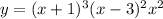A polynomial function in its factored form is written:
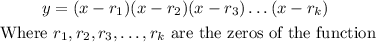
On the other hand, the number of times a given factor appears in the factored form of the equation of a polynomial is called multiplicity.
So, in this case, we have
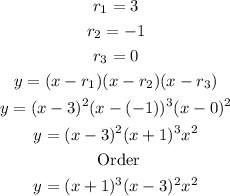
Therefore, the equation for the polynomial function (in factored form) is