Step-by-step explanation:
Let us denote by x the gallons for the first car and y the gallons for the second car.
Now, according to the problem, we have that the first car has a fuel efficiency of 20 miles per gallon of gas and the second has a fuel efficiency of 30 miles per gallon of gas and during one particular week, the two cars went a combined total of 1500 miles. Then, we get the following equation:
Equation 1:
20x + 30y = 1500
On the other hand, the problem says that there is a total gas consumption of 55 gallons. Then, we obtain the following equation:
Equation 2:
x + y = 55
From this last equation, we obtain the following equation:
Equation 3:
y = 55 - x
Now, replacing this equation in equation 1, we get:

Applying the distributive property, get
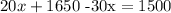
this is equivalent to:
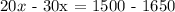
this is equivalent to:
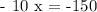
or
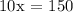
solving for x, we obtain:
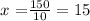
now, replacing this value in equation 3, we get:

we can conclude that the correct answer is:
Answer:
First car: 15 gallons.
Second car: 40 gallons.