Question

Suppose that $2600 is invested at an interest rate of 1.75% per year, compounded continuously. After how many years will the initial investment be doubled? Round your answer to the nearest hundredth.

Answer 1

39.61 years

Explanation:

Formula for continous compounding is given by:

`A=P\cdot e^(rt)`

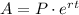
Where,

A = Future Amount: Since investement double = $2600*2 = $5200

P = Principal Amount = $2600

r = Rate of interest = 1.75% = 1.75/100 = 0.0175

t = Time in years = t

Replaicng:

`\begin{gathered} 5200=2600\cdot e^(0.0175\cdot t) \\ (5200)/(2600)=e^(0.0175\cdot t) \\ e^(0.0175t)=2 \\ 0.0175t=\ln 2 \\ t=(\ln 2)/(0.0175) \\ t=39.608\cong39.61\text{ years} \end{gathered}`

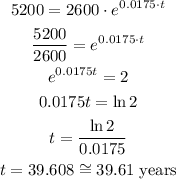
After 39.61 years the initial investment will double