Solve the polynomial equation check all solutions both real and imaginary (x^2-9)(x^2+4)=0

Question

asked Apr 23, 2023 105k views

1 Answer

Henry Moshkovich · Answer 1 · 2023-04-28T01:39:00+0000

We have the next polynomial equation

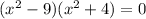
$\mleft(x^2-9\mright)\mleft(x^2+4\mright)=0$

First we will solve because if this binomial is zero all the polynomial expression is zero

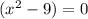
$\mleft(x^2-9\mright)=0$

$\begin{gathered} x^2=9 \\ x=\pm\sqrt[]{9} \\ x=\pm3 \end{gathered}$

the first two solutions are x=3, x=-3

For the second binomial

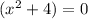
$\begin{gathered} x^2=-4 \\ x=\pm\sqrt[]{-4} \\ x\pm2i \end{gathered}$

the other solutions are x=2i, x=-2i

The solutions of the polynomial equation are

x=3

x=-3

x=2i

x=-2i